著者 とある経済学部生のデータ分析ログ
※本記事の文章・構成・分析の解釈は筆者によるオリジナルの研究成果です。
引用・紹介を行う場合は、出典(記事URLまたは著者名)を明記してください。
無断転載および無断での再配布はご遠慮ください。
※ 本記事は、note「とある経済学部生のデータ分析ログ」に公開されている「箱根駅伝 総合タイムを左右する区間は何区? ~決定木分析を用いて~」と同一のものとなっております。
noteはこちら⇒とある経済学部生のデータ分析ログ|note
皆さん、こんにちは!
記念すべき最初の記事は、お正月の風物詩、箱根駅伝についてです!
毎年1月2日、3日と箱根駅伝が開催されます。
多くの大学生ランナーが箱根駅伝に向けて、努力を積み重ねてきました。
第102回大会は、青山学院大学の優勝で幕を閉じました。
どの選手の走りも素晴らしかったですね。
今回は、データ分析を学んでいる私が、過去の箱根駅伝のデータを用いて、分析を行っていきたいと思います!
分析テーマ
箱根駅伝 総合タイムを左右するのは何区?
分析手法
・区間別の記述統計分析
各区間の平均タイムと標準偏差を算出し、差が生じやすい区間を特定する。
・決定木分析(回帰)による総合タイム分析
区間タイムを説明変数、総合タイムを被説明変数として回帰決定木分析を行い、総合タイムを左右する区間構造を可視化する。
使用データ
読売新聞オンラインの箱根駅伝特集ページ
(箱根駅伝2026最新ニュース コース・出場校など特集サイト : 読売新聞)より、第96回~第101回大会に出場した全チーム(関東学生連合含む)の総合タイムおよび各区間タイムを収集。
複数大会に出場した同一大学は大会ごとに別チームとして扱い、
全128チーム分のデータを手作業でCSV化し、分析に用いた。
分析の枠組みは上記のとおりです。
以下が目次となります!
目次
1. 区間別の記述統計分析
1.1 使用した指標と計算方法
1.1.1 区間タイムの平均値
1.1.2 区間タイムの標準偏差
1.2 分析結果:区間別 平均タイムとばらつき
1.3 記述統計分析の解釈
2. 決定木分析(回帰)による総合タイム分析
2.1 決定木分析の概要
2.2 ノードと分岐の考え方
2.3 分岐条件と True / False の意味
2.4 value・samples・squared error の意味
2.5 CARTアルゴリズムとコスト関数
2.6 本研究におけるモデル設定
3. 決定木分析の結果およびその解釈
3.1 区間タイムの特徴量重要度
3.2 決定木全体構造と3区の分岐的役割
3.3 3区が速い場合:アドバンテージを活かせる構造か
3.4 3区が速くない場合:挽回できるチームとできないチーム
3.5 3区以降の構造から得られる本質的示唆
3.6 区間別ばらつき分析を決定木結果から捉え直す視点
3.7 ばらつき分析と決定木分析が示す「重要性」の違い
3.8 なぜ3区が構造的に最重要なのか
3.9 5区・9区は「重要ではない」のか?
4. 総合的結論と今後の展望
4.1 本研究の総合的結論
4.2 本分析の意義と今後の展望
おわりに
付録
付録A squared errorを表示している木
付録B ルートノードにおける分岐結果の可視化
それでは、お楽しみください!
1.区間別の記述統計分析
まず、各区間のタイムについて、平均値および標準偏差を算出し、
区間ごとの特徴を把握する記述統計分析を行った。
1.1 使用した指標と計算方法
1.1.1 区間タイムの平均値
各区間における平均タイムは、次式で定義される。
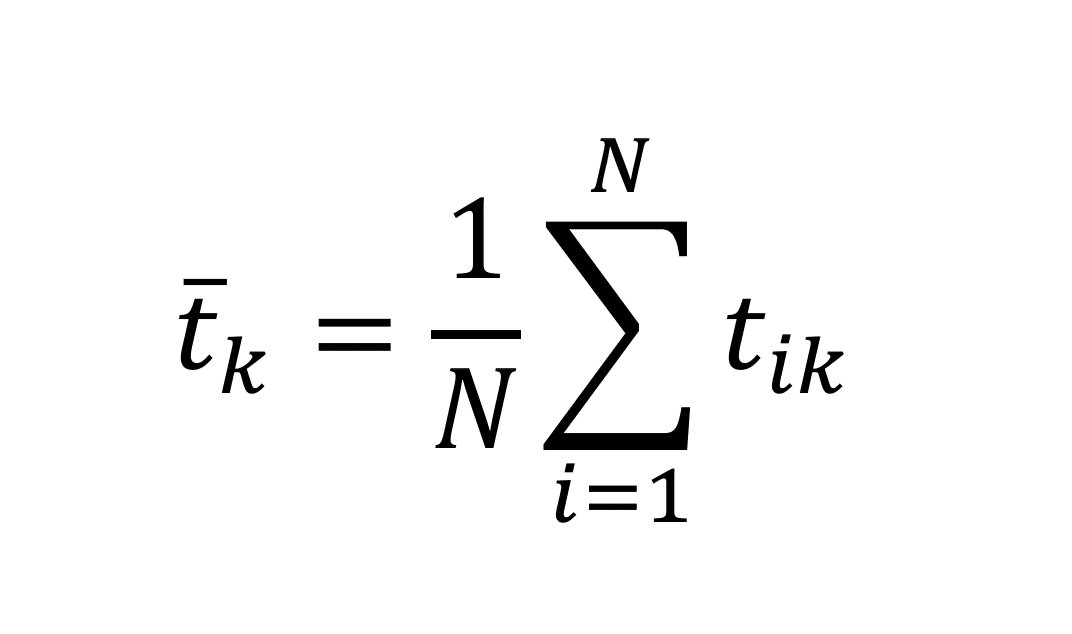
ここで、

である。
1.1.2 区間タイムの標準偏差
区間ごとのタイムのばらつきを測るため、標準偏差 σkを以下の式で算出した。
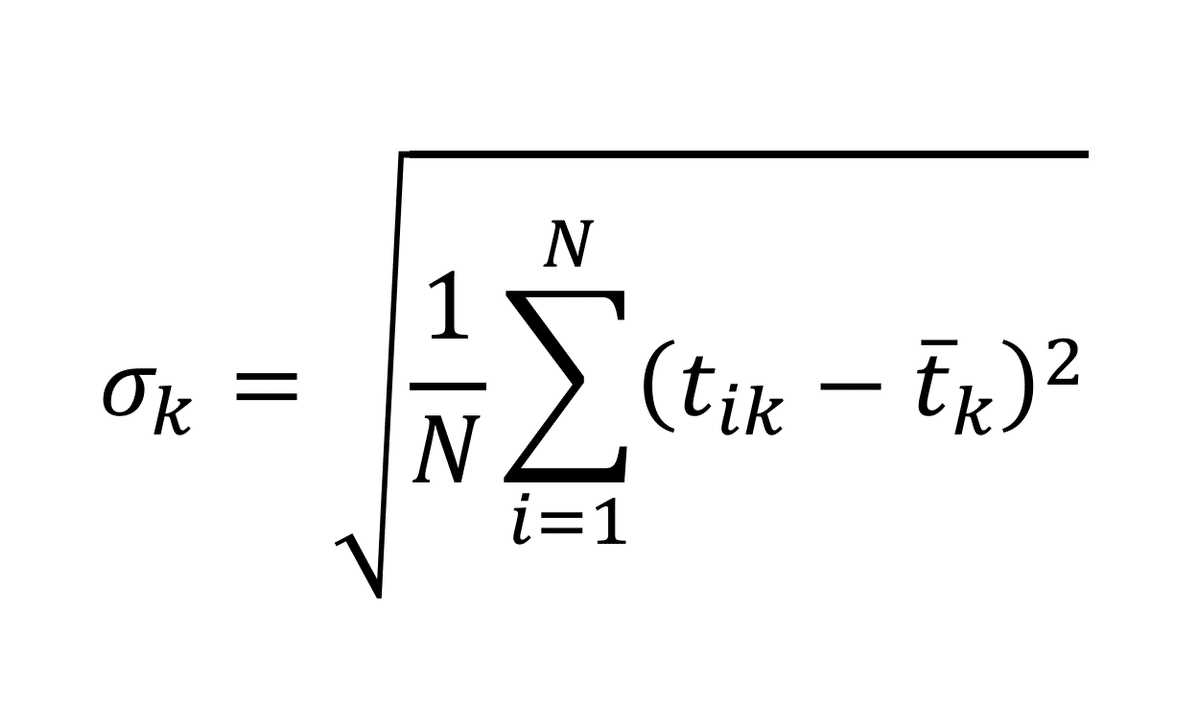
標準偏差は「その区間でどれだけ差が付きやすいか」を示す指標として解釈できる。
標準偏差が大きい区間ほど、差が生じやすく、標準偏差が小さい区間ほど、差が生じにくいと言える。
1.2 分析結果:区間別 平均タイムとばらつき(標準偏差)
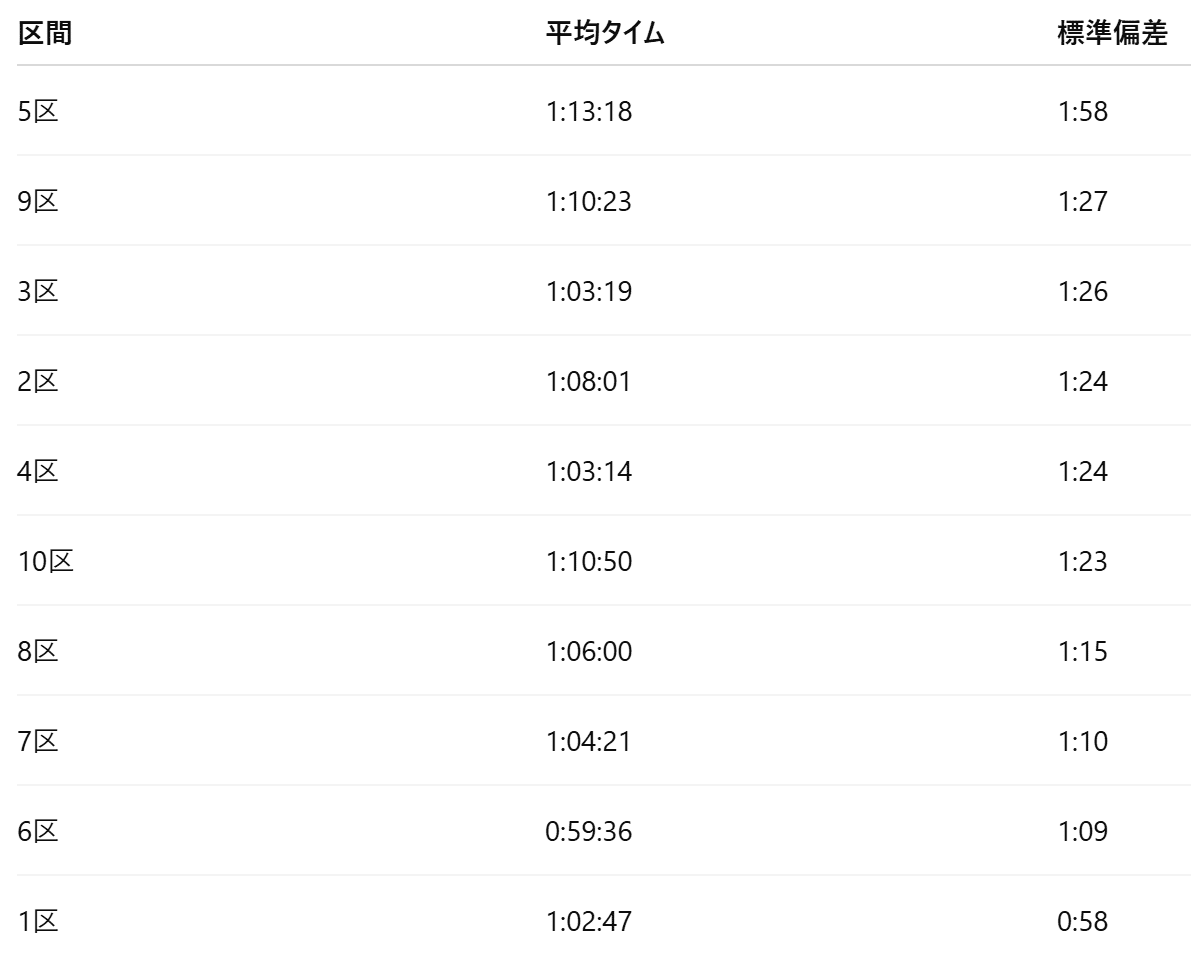
1.3 記述統計分析の解釈
分析の結果、区間ごとに標準偏差には明確な差が見られた。
例えば5区では、多くの選手の区間タイムが平均1時間13分18秒を中心に、約±1分58秒程度のばらつきを持って分布している。
このことから、5区は他の区間と比べてタイムのばらつきが大きく、差が生じやすい区間であることが分かる。
一方で1区は標準偏差が最も小さく、多くの選手の区間タイムが平均1時間2分47秒を中心に、約±58秒程度の範囲に集中している。
これは、1区では大きな差が生じにくい区間であることを意味している。
また、9区の標準偏差も比較的大きい値を示している。
よって、9区も差が生じやすい区間であるといえる。
「復路のエース」と言われる9区に力のある選手を配置できると、大きく差をつけられる可能性があることが、データからも裏付けられる。
さらに、1区を除く往路の区間(2区、3区、4区、5区)は、標準偏差が比較的大きく、これらの区間では差が生じやすい傾向が見られる。
以上より、チームの結果を大きく左右するのは往路であり、特に5区が重要な区間となってくることが分かる。
※本分析は、第96回〜101回大会に出場した全128チームの記録を統合して行っており、ここで得られた結果は、特定の大会や大学に依存しない、区間そのものが構造的に持つ「差の出やすさ」を反映したものと考えられる。
ここで、自然な疑問が生じる。
「箱根駅伝は、すべての区間を速く走れば勝つのだから、改めて分析する意味はあるのか?」
たしかに、単純な合計タイムという観点に立てば、この指摘は正しい。
全区間を通じて速いチームが上位に来ること自体は、改めて議論するまでもない事実である。
しかし、本研究で関心があるのは、
「速いかどうか」そのものではなく、
どの区間が、どの順序で、どのような条件のもとで、総合タイムに強く影響しているのかという点である。
記述統計分析によって明らかになったのは、
- 区間ごとに、タイムのばらつきには大きな差があること
- 特に往路(2区〜5区)や9区では、差が生じやすい構造を持っていること
であった。
しかし、この分析だけでは、
- それらの区間が 総合タイムに対して、どの程度決定的なのか
- 複数の区間が どのような順序で影響し合っているのか
- ある区間が速い(あるいは遅い)場合に、他の区間がどのような役割を果たすのか
といった点までは明らかにできない。
そこで次章では、
区間タイムを説明変数、総合タイムを被説明変数とした 回帰決定木分析を用い、
- どの区間が総合タイムを最も左右しているのか
- どの区間を、どの水準のタイムで走ると、総合タイムに大きな差が生じるのか
- 区間同士がどのような条件付き構造を持っているのか
を、分岐構造として可視化し、より踏み込んだ分析を行う。
2.決定木分析(回帰)による総合タイム分析
本章では、各区間のタイムが箱根駅伝の総合タイムにどのような影響を与えているのかを明らかにするため、回帰決定木(Decision Tree Regression)を用いた分析を行う。
本研究の主な関心は、
- どの区間が総合タイムを最も大きく左右しているのか
- どの区間を、どの程度のタイムで走ることが総合成績に影響するのか
という点にある。
決定木分析は、これらの問いに対して
重要な区間と、その分岐点(閾値)を明示的に示すことができる
という特徴を持ち、本研究の目的に適した手法である。
2.1 決定木分析の概要
決定木分析とは、説明変数の値に基づいてデータを段階的に分割し、被説明変数を予測する手法である。
本研究では、被説明変数が連続値であるため、回帰決定木を用いる。
回帰決定木は、各区間のタイムを条件としてチームのデータを分割し、その分割を繰り返すことで、最終的に総合タイムの代表値を予測する構造を持つ。
決定木の特徴として、
- 分析結果を図として可視化できること
- 「どの区間が」「どの水準で」重要かを直感的に理解できること
が挙げられる。
2.2 ノードと分岐の考え方
決定木は、複数の ノード(node) から構成される。
- ルートノード
すべてのチームを含む最上位のノードであり、
総合タイムを最もよく分割する区間と閾値が配置される。 - 内部ノード
「○区のタイムが◯分◯秒以下かどうか」といった条件により、
データをさらに分割するための分岐点となるノードである - リーフノード(終端ノード)
これ以上分割されないノードであり、
その条件を満たすチーム群における 総合タイムの平均値 が示される。
各ノードは、
「それまでの分岐条件をすべて満たすチームの集合」を表している。
以上を踏まえ、以下に本研究で推定した回帰決定木の一部を示す。

画像の四角が、ノードである。
2.3 分岐条件と True / False の意味
各ノードの上部には、次のような分岐条件が表示されている。
3区 ≤ 1:02:46
これは、
「3区の区間タイムが1時間2分46秒以下であるかどうか」
を意味する。
- 条件を満たす場合 → True(左側の枝)
- 条件を満たさない場合 → False(右側の枝)
という形で各チームが分割される。
2.4 value ・ samples・ squared error の意味
決定木の各ノードには、以下の情報が表示されている。
- value
そのノードに属するチーム群の 総合タイムの平均値 を表す。
これは予測値(代表値)であり、個別チームの記録ではない。 - samples
そのノードに含まれるチーム数を表す。 - squared error
ノード内における総合タイムのばらつきを示す指標であり、
平均二乗誤差に対応する。
2.5 CARTアルゴリズムとコスト関数
本研究では、回帰決定木アルゴリズムとして
CART( Classification and Regression Trees) を用いる。
CART回帰木では、各ノードに属するチーム集合における
被説明変数(本研究では総合タイム)のばらつきを、
squared error(平均二乗誤差)によって評価する。
あるノード R に含まれるチーム集合に対し、
ノード内の squared error は次式で定義される。
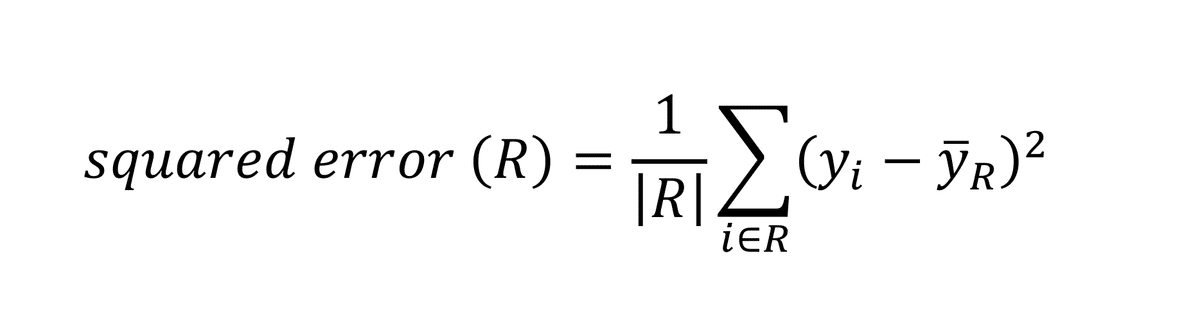
ここで、

を表す。
CARTでは、単一ノードの誤差ではなく、
分割後の左右ノードにおける誤差の加重平均を評価基準として用いる。

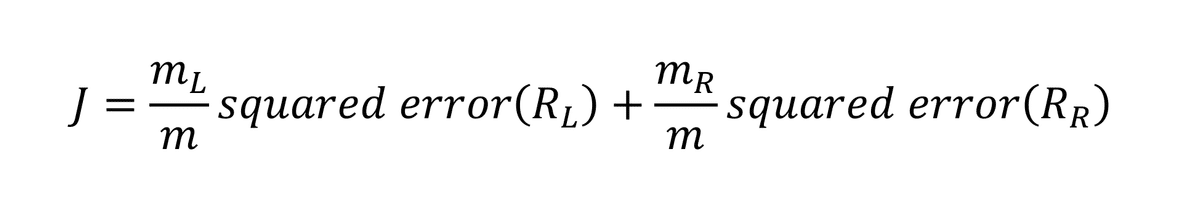
ここで、

を表す。
CARTは、各ノードにおいて
このコスト関数 J が最小となるような
区間(説明変数)および閾値を自動的に選択し,
決定木を逐次的に構築する。
2.6 本研究におけるモデル設定
本研究では、
- 被説明変数:総合タイム
- 説明変数:1区〜10区の各区間タイム
を用いて回帰決定木を構築した。
また、結果の解釈性を重視し、
過度に複雑な分岐による過学習を避けるため、
決定木の深さは最大4に制限している。
3. 決定木分析の結果およびその解釈
本節では、回帰決定木の推定結果をもとに、
どの区間が総合タイムを左右しているのか、
どの程度の区間タイムが分岐点となっているのか
について解釈を行う。
3.1 区間タイムの特徴量重要度
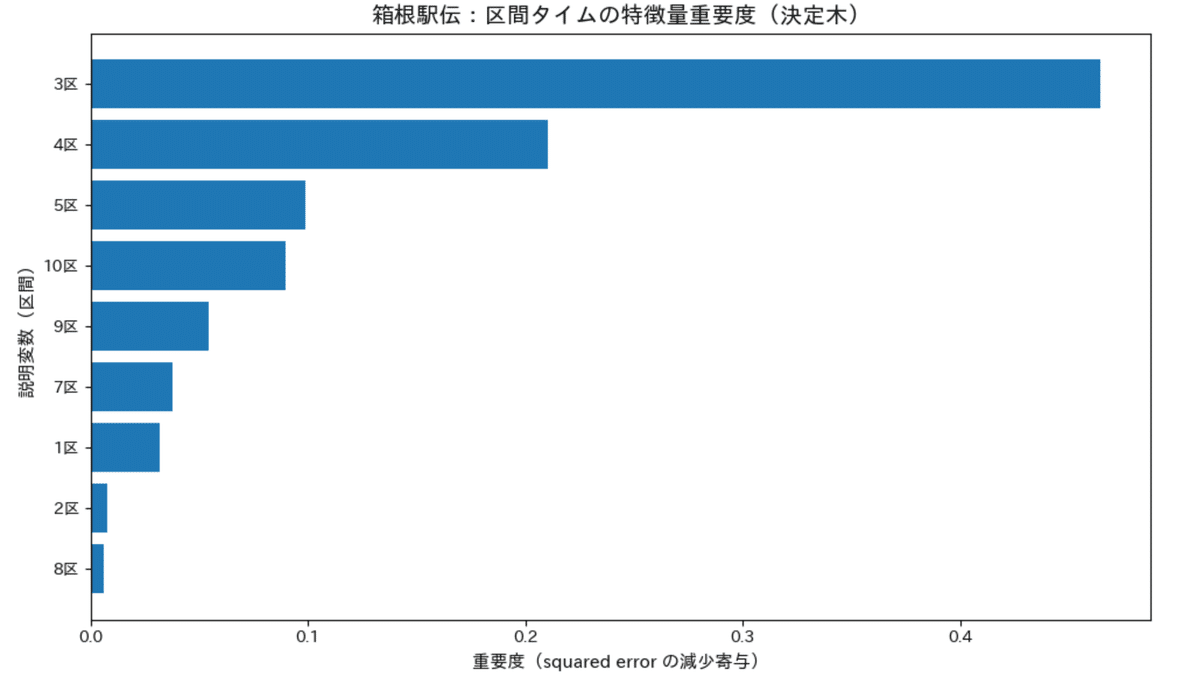
まず、決定木における特徴量重要度(squared error の減少への寄与)を見ると、3区の重要度が突出して高いことが分かる。
重要度は、
「その区間が分岐に用いられることで、どれだけ squared error を減少させたか」
を表しており、値が大きいほど、決定木モデルにおいて総合タイムの予測に強く寄与していることを意味する。
本分析では、
- 3区が最も高い重要度
- 次いで 4区、5区、10区 が続く
- それ以外の区間は相対的に寄与が小さい
という結果が得られた。
このことから、
箱根駅伝の総合タイムは、すべての区間が等しく効いているわけではなく、
特に3区を中心とした一部の区間が強く影響している
ことが示唆される。
3.2 決定木全体構造と3区の分岐的役割
木構造を可視化する。
以降、ノードのオレンジ色が濃いほど、value値が小さい、つまり総合タイムが速いノードである。
今回、squared errorは結果を解釈する上で重要ではないので、木構造を見やすくするために、squared errorを取り除いた。
(squared errorを表示している木は、付録へ)
分析結果がこちら。
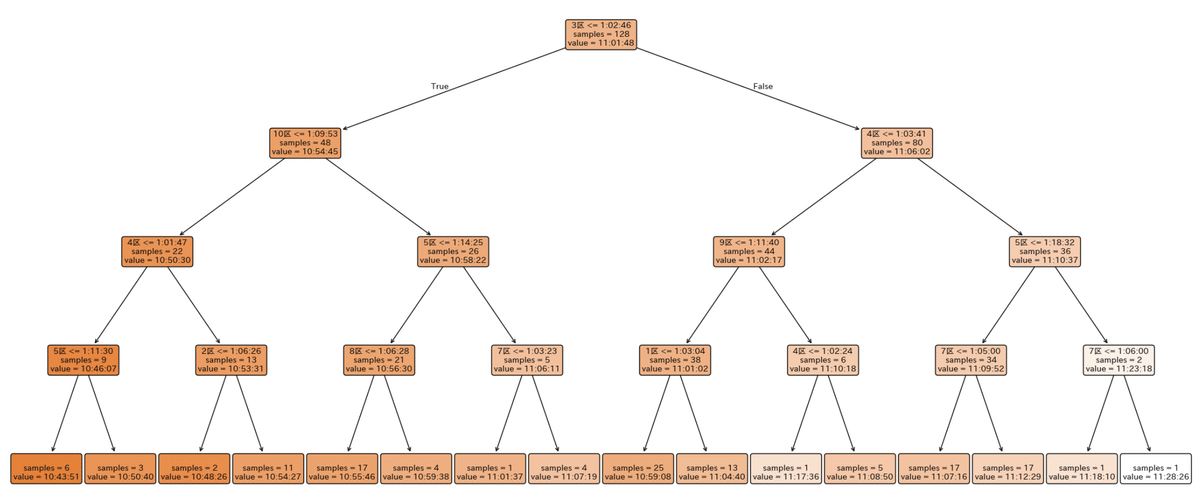
最初の分岐条件付近を拡大したものはこちら。
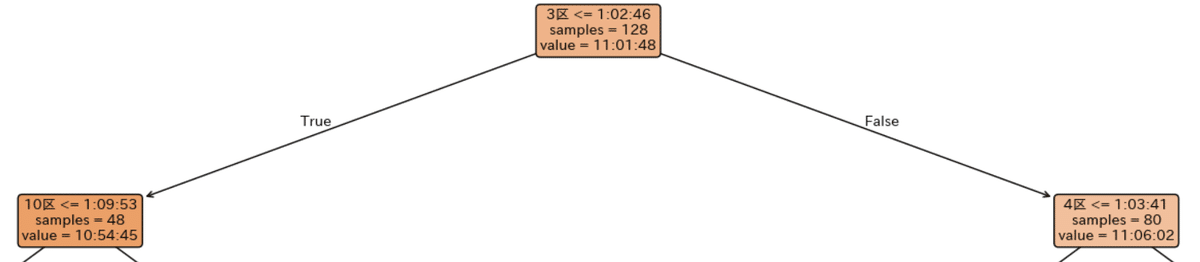
決定木の構造を見ると、最上位(ルート)ノードにおいて
3区 ≤ 1:02:46
という条件が最初に選択されている。
決定木では、
最初に分岐する変数が、総合タイムのばらつきを最も大きく減少させる変数であるため、この結果は
3区が総合タイムを最も左右する区間である
ことを意味している。
実際に、3区の条件によって分かれた2つのグループの平均総合タイムは、
- 3区 ≤ 1:02:46:平均 10:54:45
- 3区 > 1:02:46:平均 11:06:02
となっており、その差は 約11分 にも及ぶ。
これは、単一区間のタイム差としては極めて大きく、
3区が総合成績の大きな境目となっていることを強く示している。
しかし、決定木が示しているのは
「3区だけで全てが決まる」という単純な構造ではない。
重要なのは、3区の結果を、その後の区間でどう扱っているかである。
3.3 3区が速い場合:アドバンテージを活かせる構造か
木構造の左側を拡大したものはこちら。
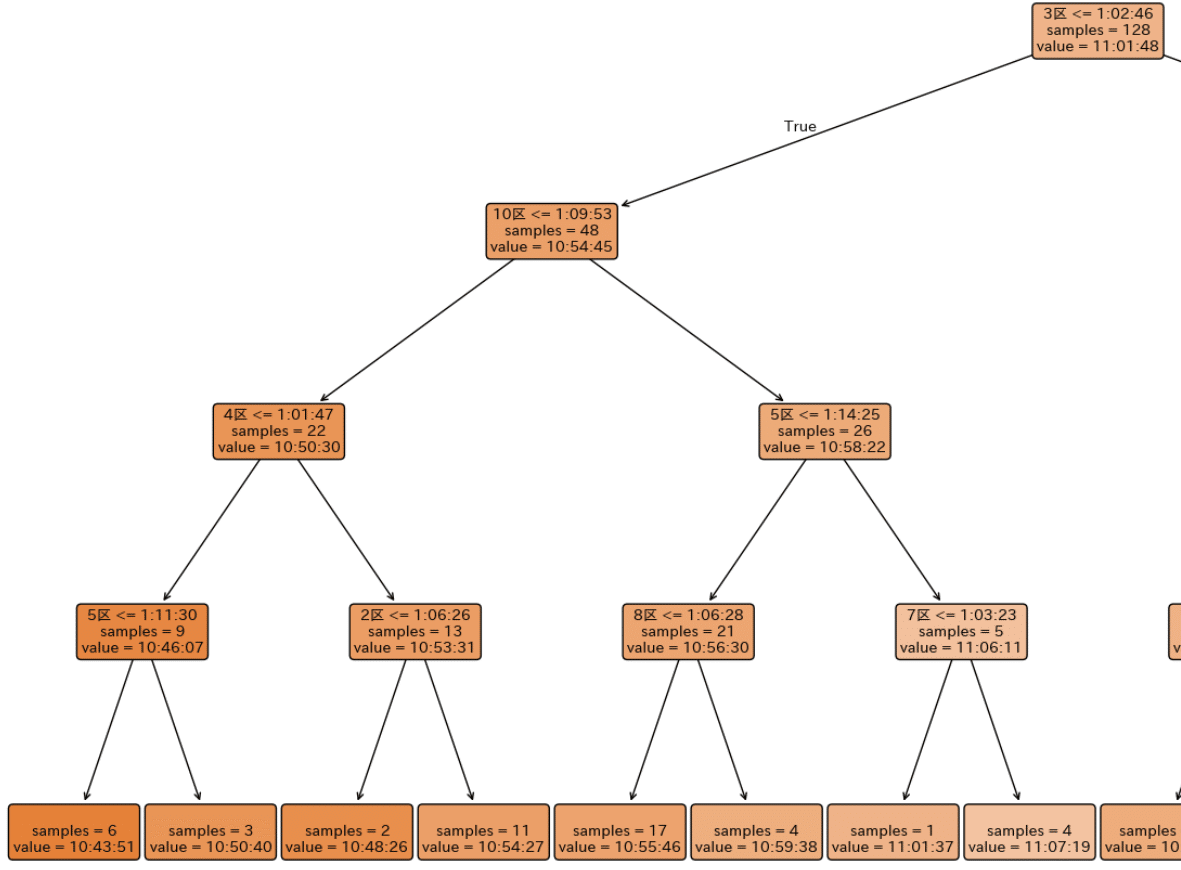
まず、3区 ≤ 1:02:46 を満たしたチーム群(左側ノード)を見る。
この集団の平均総合タイムは 10:54:45 と、
全体平均(11:01:48)を大きく下回っている。
次に効いているのは「10区」
3区が速い集団では、次の分岐として
10区 ≤ 1:09:53
が現れている。
これは、
3区で得たアドバンテージを、最終10区で維持できているか
が次の重要な判断基準になっていることを意味する。
さらに分かれる「4区・5区」の役割
10区の条件を満たしたチームの中でも、
- 4区 ≤ 1:01:47
- 5区 ≤ 1:11:30
といった条件を同時に満たす場合、
平均総合タイムは 10時間43分台 にまで到達している。
この構造は、
「3区が速いだけでは不十分で、
他の主要区間である4区、5区をしっかりまとめられているか」
が上位帯への条件であることを示している。
一方で、3区が速くても、
- 5区や7区で基準を超える
- 10区で失速する
といったケースでは、
総合タイムは 11時間前後 まで押し戻されている。
3区の速さは“必要条件”だが“十分条件”ではない
という点が、決定木から明確に読み取れる。
3.4 3区が速くない場合:挽回できるチームとできないチーム
木構造の右側を拡大したものはこちら。
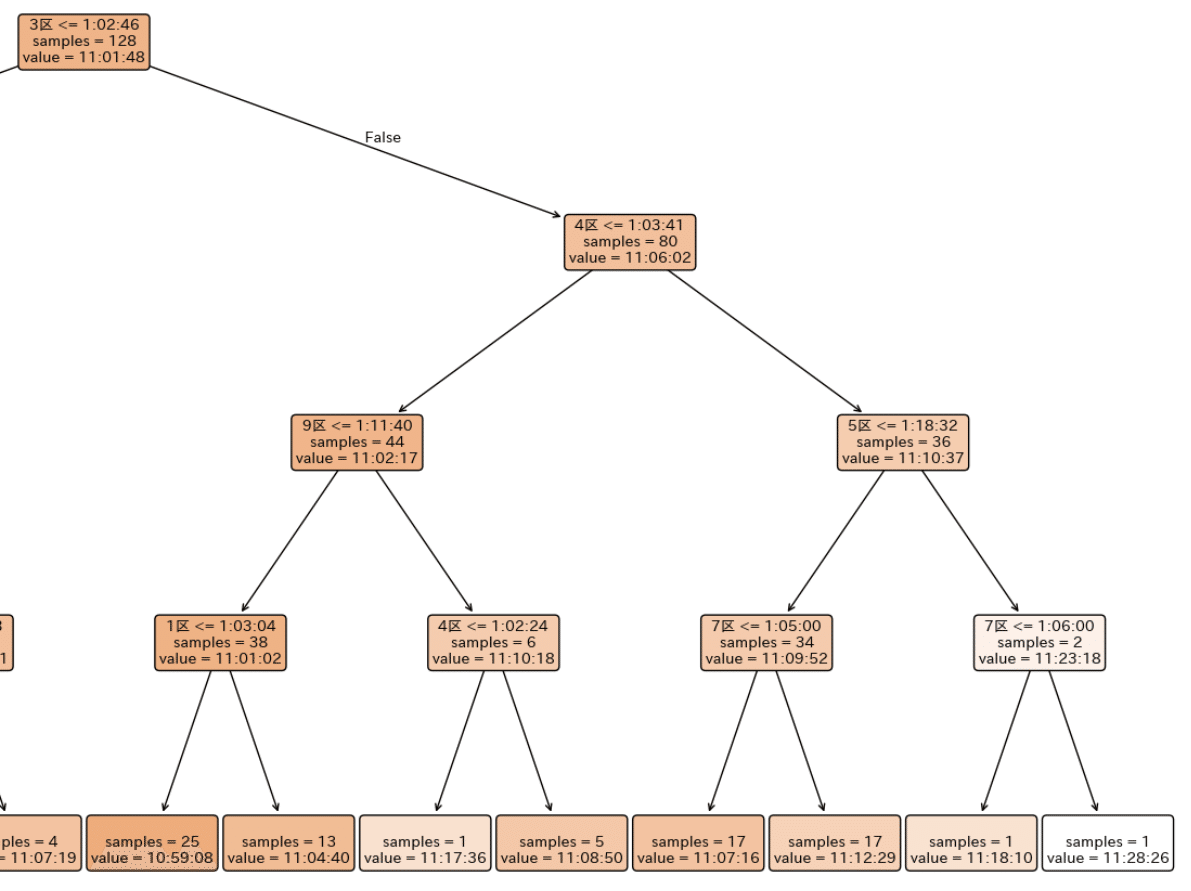
次に、3区 > 1:02:46 のチーム群(右側ノード)を見ていく。
この集団の平均総合タイムは 11:06:02 である。
まず問われるのは「4区での踏ん張り」
この側では、次の分岐として
4区 ≤ 1:03:41
が現れている。
これは、
3区で遅れた後、その流れを4区で止められているか
が最初の分かれ道であることを意味する。
4区を耐えた場合:9区・1区による回復余地
4区の条件を満たしたチームでは、
さらに 9区 ≤ 1:11:40 や 1区 ≤ 1:03:04 といった分岐が続く。
これらを満たした場合、
平均総合タイムは 11時間をわずかに下回る水準まで回復しており、
3区の遅れは、後続区間の安定によって部分的に挽回可能
であることが示されている。
4区を耐えられなかった場合:5区・7区での悪化
一方、4区で基準を超えたチームでは、
- 5区 ≤ 1:18:32
- 7区 ≤ 1:05:00
といった条件でさらに分岐し、
総合タイムは 11時間10分超 の領域に集中していく。
この構造は、
3区の遅れに4区・5区・7区の不安定さが重なると、
総合タイムの悪化が連鎖的に進む
ことを示している。
3.5 3区以降の構造から得られる本質的示唆
以上を踏まえると、決定木分析の結果は、次のような構造的特徴を示している。
- 3区は総合タイムの初期条件を決める最重要区間である
- 3区が速い場合でも、
10区・4区・5区を安定させなければ上位帯には到達しない - 3区が遅れた場合でも、
4区を起点とした後続区間の粘りによって、一定の挽回は可能である - 総合タイムの大きな悪化は、
3区の遅れと複数区間の不安定さが重なったときに生じる
決定木分析により、
「どの区間が重要か」だけでなく、
「区間同士がどの順序で影響し合っているか」
という構造を明示的に捉えることができた。
3.6 区間別ばらつき分析を決定木結果から捉え直す視点
ここで、記事前半で示した
**区間別の平均タイムとばらつき(標準偏差)**の結果を改めて振り返る。
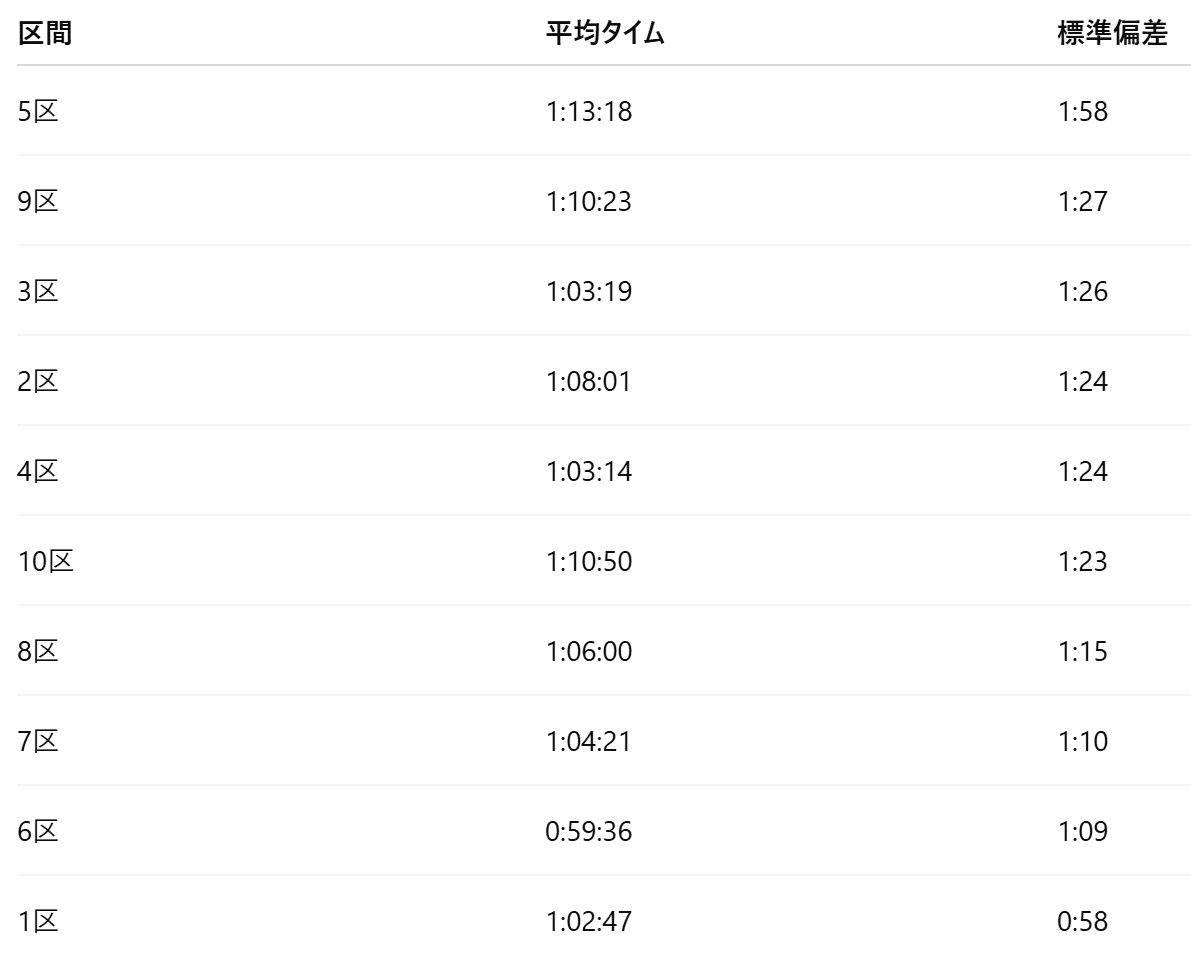
前半の分析では、標準偏差の大きい順に、
- 5区
- 9区
- 3区
- 2区・4区
- 10区
といった区間が、タイムのばらつきが大きい区間として確認されていた。
この結果は一見すると、
「5区や9区の方が3区より重要なのではないか」
という印象を与える可能性がある。
しかし、決定木分析の結果と照らし合わせることで、
この見方はより立体的に理解できる。
3.7 ばらつき分析と決定木分析が示す「重要性」の違い
標準偏差が大きいということは、
その区間において、タイムの差が出やすいことを意味する。
実際に、5区や9区はコース特性や距離の影響が大きく、
個々の走者の出来不出来がタイムに反映されやすい区間である。
一方で、決定木分析が示したのは、
「どの区間が最初に総合タイムの運命を分けるか」
という構造である。
その結果、
- 標準偏差では3位程度であった 3区 が
- 決定木では 最初の分岐(最重要区間) として選択された
という違いが生じた。
これは、
「ばらつきが大きい区間」=重要
では必ずしもない
ことを意味している。
3.8 なぜ3区が「構造的に最重要」なのか
決定木の結果から明らかになったのは、
3区が単にタイムのばらつきを持つ区間ではなく、
- その後の区間構成
- チーム全体の流れ
- 総合タイムの初期水準
を決定づける 起点(初期条件) として機能している点である。
3区で 1:02:46 を切れるかどうかによって、
- その後に「上位帯に進む可能性が開くチーム」
- あるいは「後続区間で挽回を強いられるチーム」
が明確に分岐していた。
これは、
前半の平均・標準偏差分析だけでは捉えきれなかった
区間同士の順序関係と条件付き構造を、
決定木が可視化した結果である。
3.9 5区・9区は「重要ではない」のか?
ここで注意すべきなのは、
5区や9区が重要でない、という結論ではない点である。
決定木の構造を見ると、
- 3区が速い場合
→ 5区・10区・4区が上位帯到達の条件として現れる - 3区が遅れた場合
→ 4区を起点に、9区・5区・7区が挽回・悪化を左右する
という形で、
5区・9区は「条件付きで強く効く区間」として登場している。
つまり、
- 5区・9区は「単体ではばらつきが大きい」
- しかし 3区という初期条件の後で初めて意味を持つ
という位置づけにある。
この点で、
標準偏差分析(区間単体におけるタイムのばらつき)と
決定木分析(区間間の構造)は、
互いに補完的な関係にあると言える。
4. 総合的結論と今後の展望
本章では、これまでの分析結果を総括し、本研究から得られた知見を整理するとともに、今後の課題と展望について述べる。
4.1 本研究の総合的結論
以上の分析から、次の結論が導かれる。
- 箱根駅伝の総合タイムへは、
すべての区間が同列に重要なのではない - 3区は総合タイムの初期条件を決定する構造的に最重要な区間である
- 5区・9区などばらつきの大きい区間は、条件付きで総合タイムを左右する
- 総合タイムの大きな悪化は、
初期条件(3区の遅れ)と複数区間の不安定さが重なったときに生じる
決定木分析を用いることで、「どの区間が重要か」だけでなく、
「区間同士がどの順序で影響し合っているか」
という構造を、具体的な数値と分岐条件として示すことができた。
4.2 本分析の意義と今後の展望
本研究の意義は、箱根駅伝という長距離駅伝を対象に、
区間を単体で評価する視点から、区間同士の関係性と順序構造を捉える視点へと分析を拡張した点にある。
本研究では、決定木分析を用いることで、
- どの区間が 最初に総合タイムの方向性を分けるのか
- その後、どの区間が 条件付きで影響力を持つのか
という 構造的・条件付きな関係を明示的に捉えることができた。
この点は、「全区間が重要である」という一般論を否定するものではなく、
現実の制約下において、どの区間がどの段階で重要性を持つのかを具体化した点に本研究の特徴がある。
一方で、本研究は区間タイムという数値情報のみに基づく分析であり、
選手配置、チーム戦略、区間間の心理的影響などは直接的には扱っていない。
今後は、区間間の連鎖や相互作用をより明確に捉える手法として、
ネットワーク分析などを用いた拡張的分析を行うことで、
駅伝における「流れ」の理解をさらに深めたいと思う。
おわりに
本研究では、箱根駅伝の区間タイムデータを用い、
決定木分析によって総合タイムの構造を可視化した。
その結果、3区を起点とする条件付きの分岐構造が、
総合成績の流れを大きく左右していることが明らかになった。
箱根駅伝は、「どこか一つの区間だけを速くすれば勝てる」競技ではない。
しかし同時に、「流れを決める区間」が確かに存在する競技でもある。
決定木分析は、そのような駅伝特有の構造を、
感覚や経験則ではなく、具体的な分岐条件として示すことができる
有効な手法であることが、本研究から示唆された。
本研究が、箱根駅伝をより深く楽しむ一助となれば幸いである。
今後の箱根駅伝のさらなる発展と、ランナーの皆さんの快走を願い、本研究を締めくくりたい。
今後もさまざまなデータを用いて、分析を行っていきます。
興味を持っていただけた方は、ぜひ引き続きチェックお願いします!
付録
付録A squared errorを表示している木
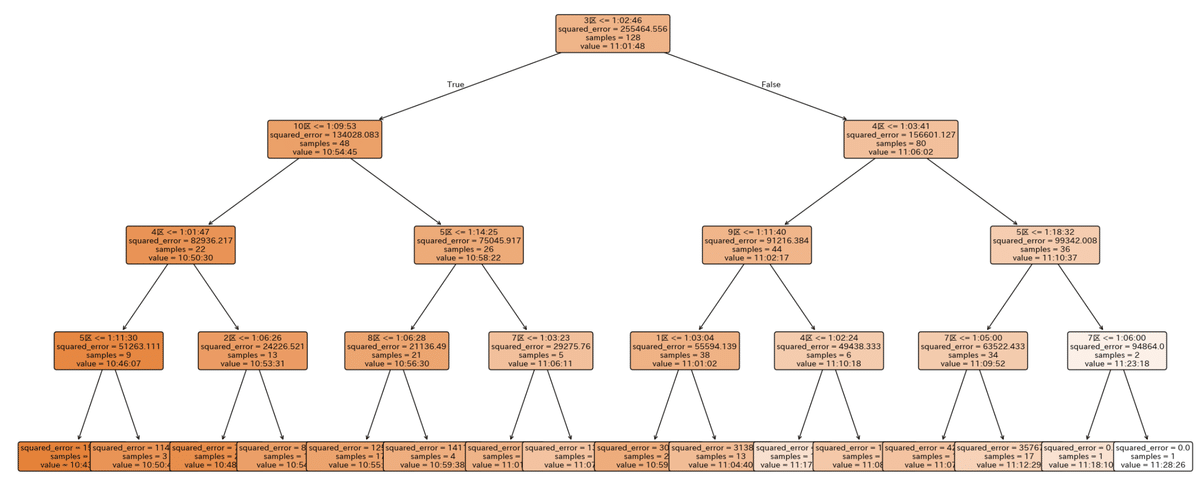
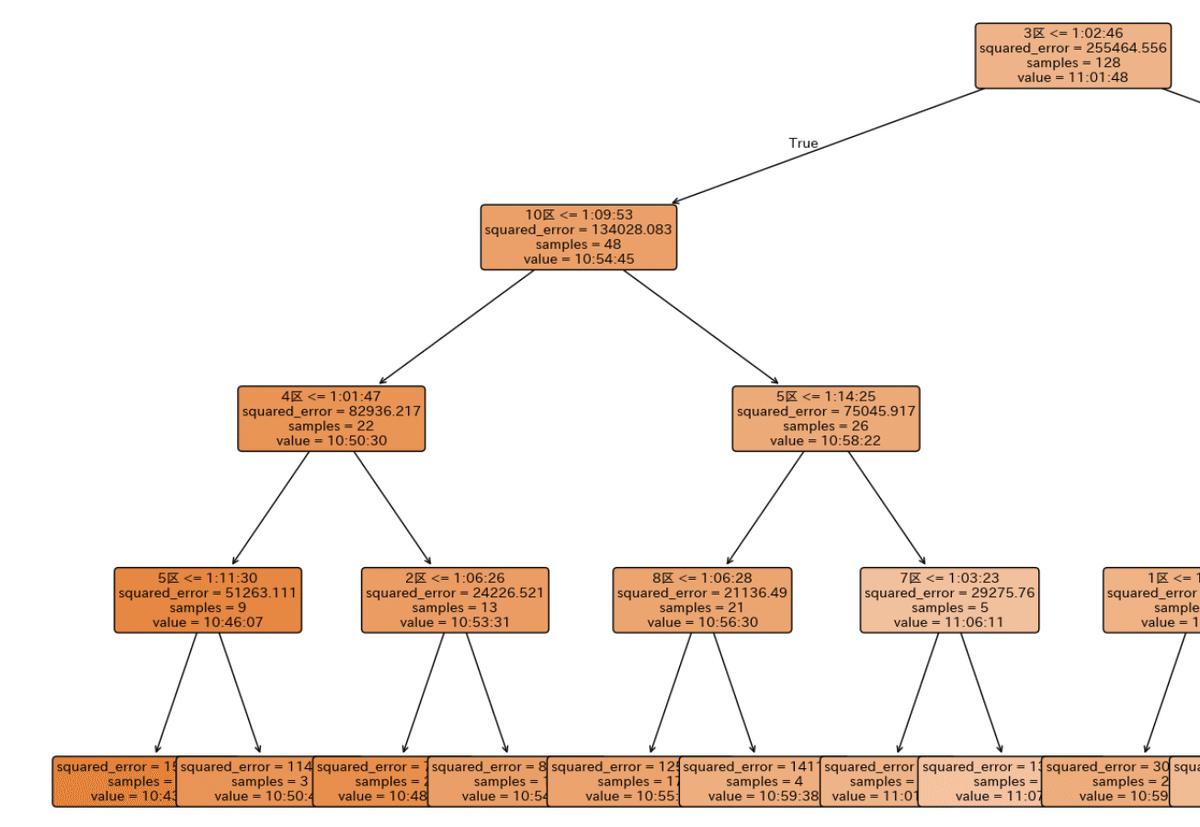
左側を拡大
右側を拡大
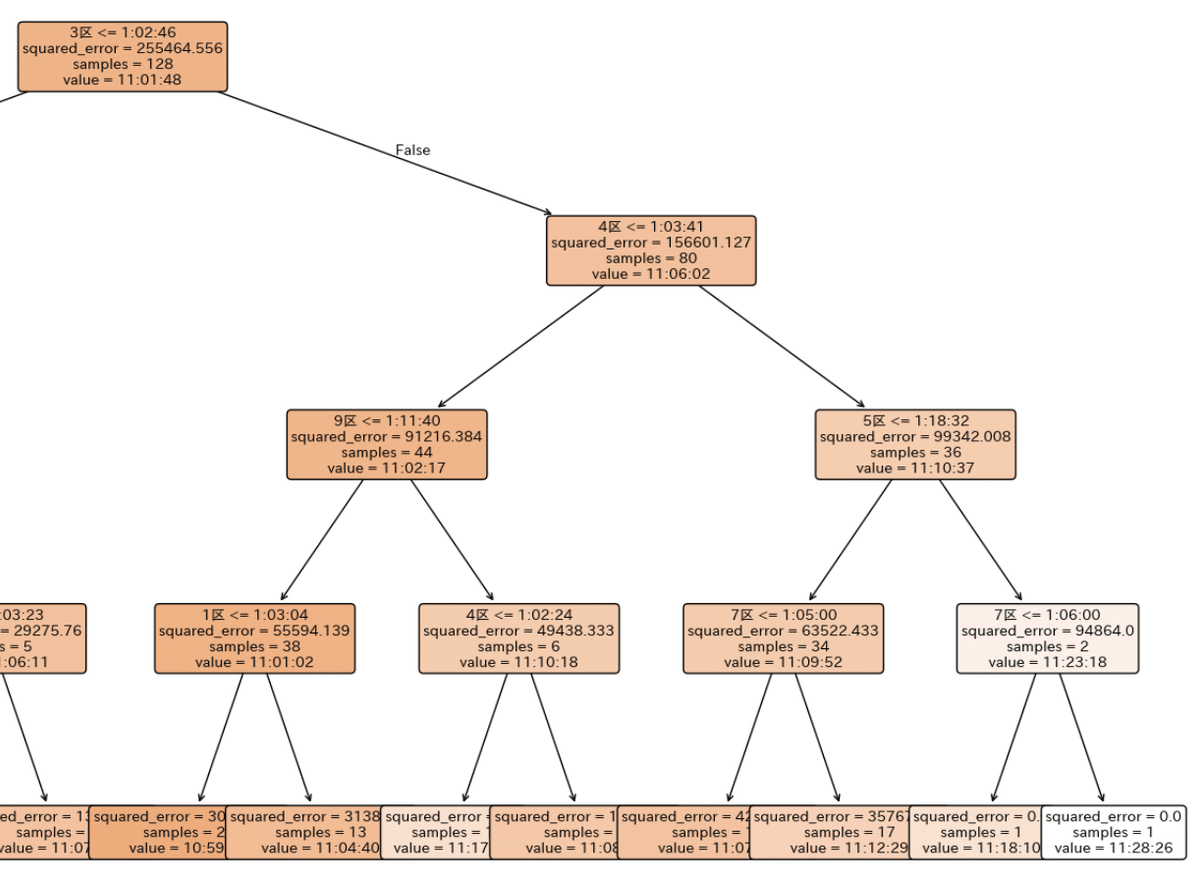
(被って見えない部分があります。ご了承ください。)
付録B ルートノードにおける分岐結果の可視化